2. Описание системы массового обслуживания.
В математических моделях (ММ) сложных объектов, представленных в виде систем массового обслуживания (СМО), фигурируют средства обслуживания, называемые обслуживающими аппаратами (ОА), и обслуживаемые заявки, называемые транзактами. Так, в моделях систем обработки и передачи данных ОА отображают микропроцессоры и линии связи, а транзакты - поступающие на обработку заявки и пакеты данных.
Состояние СМО характеризуется состояниями ОА, транзактов и очередей к ОА. Состояние ОА описывается двоичной переменной, которая может принимать значения "занят" или "свободен". Переменная, характеризующая состояние транзакта, может иметь значения "обслуживания" или "ожидания". Состояние очереди характеризуется количеством находящихся в ней транзактов.
Имитационная модель СМО представляет собой алгоритм, отражающий поведение СМО, т.е. отражающий изменения состояния СМО во времени при заданных потоках заявок, поступающих на входы системы. Параметры входных потоков заявок - внешние параметры СМО. Выходными параметрами являются величины, характеризующие свойства системы - качество ее функционирования. Примеры выходных параметров: производительность СМО - среднее число заявок, обслуживаемых в единицу времени; коэффициенты загрузки оборудования - отношение времен обслуживания к общему времени в каждом ОА; среднее время обслуживания одной заявки. Основное свойство ОА, учитываемое в модели СМО, - это затраты времени на обслуживание, поэтому внутренними параметрами в модели СМО являются величины, характеризующие это свойство ОА. Обычно время обслуживания рассматривается, как случайная величина и в качестве внутренних параметров фигурируют параметры законов распределения этой величины.
Имитационное моделирование позволяет исследовать СМО при различных типах входных потоков и интенсивностях поступления заявок на входы, при вариациях параметров ОА, при различных дисциплинах обслуживания заявок. Дисциплина обслуживания - правило, по которому заявки поступают из очередей на обслуживание. Величина, характеризующая право на первоочередное обслуживание, называется приоритетом. В моделях СМО заявки, приходящие на вход занятого ОА, образуют очереди, отдельные для заявок каждого приоритета. При освобождении ОА на обслуживание принимается заявка из непустой очереди с наиболее высоким приоритетом.
Основной тип ОА - устройства, именно в них происходит обработка транзактов с затратами времени. К ОА относятся также накопители (памяти), отображающие средства хранения обрабатываемых данных в вычислительных системах. Накопители характеризуются не временами обслуживания заявок, а емкостью - максимально возможным количеством одновременно находящихся в накопителе заявок.
К элементам имитационных моделей СМО кроме ОА относят также узлы и источники заявок. Связи ОА между собой реализуют узлы, т.е. характеризуют правила, по которым заявки направляются к тому или иному ОА.
Для описания моделей СМО при их исследовании на ЭВМ разработаны специальные языки имитационного моделирования. Существуют общецелевые языки, ориентирован-ные на описание широкого класса СМО в различных предметных областях, и специали-зированные языки, предназначенные для анализа систем определенного типа. Примером общецелевых языков служит широко распространенный язык GPSS.
Для описания имитационной модели на языке GPSS полезно представить ее в виде схемы, на которой отображаются элементы СМО - устройства, накопители, узлы и источники. Описание на языке GPSS есть совокупность операторов (блоков), характеризующих процессы обработки заявок. Имеются операторы и для отображения возникновения заявок, задержки их в ОА, занятия памяти, выхода из СМО, изменения параметров заявок (например, приоритетов), вывода на печать накопленной информации, характеризующей загрузку устройств, заполненность очередей и т.п.
Пути продвижения заявок между ОА отображаются последовательностью операторов в описании модели на языке GPSS специальными операторами передачи управления (перехода). Для моделирования используется событийный метод. Соблюдение правильной временной последовательности имитации событий в СМО обеспечивается интерпретато-ром GPSS World - программной системой, реализующий алгоритмы имитационного моделирования.
2.1. Построение структурной схемы модели.
Имеется система передачи данных, состоящая из:
• 3-х пунктов–накопителей A,B и C
• 4-х линий AB1, AB2, BC1 и BC2
Причем пакеты данных из AB1 поступают в BC1, а из AB2 соответственно в BC2.
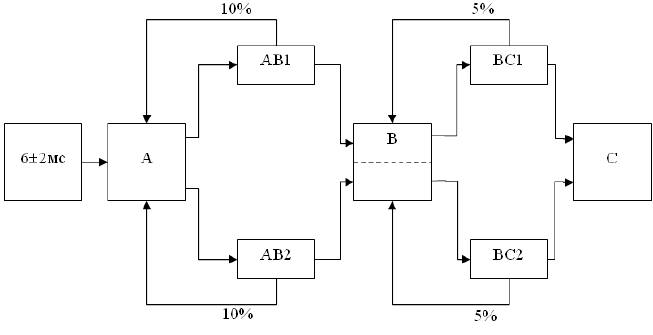
Система передачи данных обеспечивает передачу пакетов данных из пункта A в пункт C через промежуточный пункт B. В пункт А пакеты поступают через 6±2мс. Там они буферизуются и передаются по любой из двух линий. В пункте В они снова буферизуются и передаются по следующим линиям в пункт C. Во время передачи пакетов по линия возможны сбои, вероятности которых отображены на схеме.
Требуется смоделировать прохождение через систему 500 пакетов данных и определить максимальные объемы буферов в пунктах A и B, и характеристики их заполнения.
2.2. Описание сети в виде системы массового обслуживания.
В данной модели системы передачи данных, представляем:

пункты – статистические объекты типа очередь;
линии – аппаратные объекты типа прибор;
пакеты данных – транзакты.
За единицу модельного времени (е.м.в.) принята 1мс.
2.3. Формализация и алгоритмизация модели.
Формально схема модели имеет вытянутый вид с некоторым количеством узлов (переходов). Это делается для реализации передачи пакетов по четырем линиям и моделирования сбоев в них.
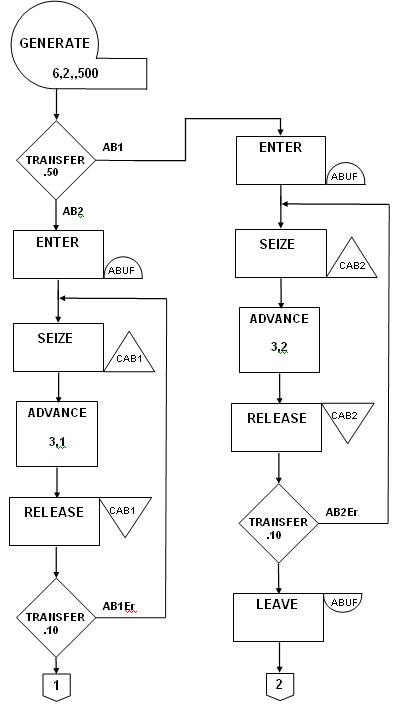
Алгоритм.
1. Генерация транзакта через 6±2 е.м.в.
2. Равновероятная передача заявок: АВ1 – переход в пункт 3; АВ2 – переход в пункт 16.
3. Вход в пункт - накопитель А.
4. Занятие линии АВ1.
5. Передача транзакта по линии АВ1 за 3±1 е.м.в. (ожидание).
6. Освобождение линии АВ1.
7. Сбой линии АВ1: 10% переходит в пункт 4.
8. Выход из пункта - накопителя А.
9. Вход в пункт - накопитель В.
10. Занятие линии ВС1.
11. Передача транзакта по линии ВС1 за 3 е.м.в. (ожидание).
12. Освобождение линии ВС1.
13. Сбой линии ВС1: 5% переходит в пункт 10.
14. Выход из пункта - накопителя В.
15. Без условная передача транзактов в пункт 28.
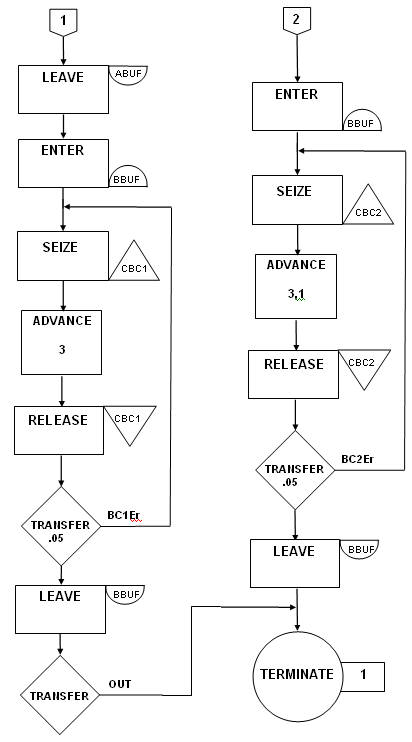
16. Вход в пункт - накопитель А.
17. Занятие линии АВ2.
18. Передача транзакта по линии АВ2 за 3±2 е.м.в. (ожидание).
19. Освобождение линии АВ2.
20. Сбой линии АВ2: 10% переходит в пункт 17.
21. Выход из пункта - накопителя А.
22. Вход в пункт - накопитель В.
23. Занятие линии ВС2.
24. Передача транзакта по линии ВС2 за 3±1 е.м.в. (ожидание).
25. Освобождение линии ВС2.
26. Сбой линии ВС2: 5% переходит в пункт 23.
27. Выход из пункта - накопителя В.
28. Удаление транзакта из модели.
29. Повторение 1-28 пока через пункт 28 не проследует 500 транзактов.
Блок схема модели.
2.4. Имитационный эксперимент.
2.4.1. Текст программы.
* V #16
* Объявление имен
*
ABUF equ 1
BBUF equ 2
CAB1 equ 1
CAB2 equ 2
CBC1 equ 3
CBC2 equ 4
ABUF STORAGE 3
BBUF STORAGE 8
*
* Основной сегмент модели
*
GENERATE 6,2,,500 ; Ввод пакетов в модель
TRANSFER .50,AB1,AB2 ; Передача на CAB1 и CAB2
AB1 ENTER ABUF ; Вход в пункт А
AB1Er SEIZE CAB1 ; Линия AB1
ADVANCE 3,1 ; Время передачи по AB1
RELEASE CAB1 ; Линия AB1
TRANSFER .10,,AB1Er ; Передача на AB1Er
LEAVE ABUF ; Выход из пункта А
ENTER BBUF ; Вход в пункт B
BC1Er SEIZE CBC1 ; Линия BC1
ADVANCE 3 ; Время передачи по BC1
RELEASE CBC1 ; Линия BC1
TRANSFER .05,,BC1Er ; Передача на BC1Er
LEAVE BBUF ; Выход из пункта B
TRANSFER ,OUT ; Передача пакетов на метку
AB2 ENTER ABUF ; Вход в пункт А
AB2Er SEIZE CAB2 ; Линия AB2
ADVANCE 3,2 ; Время передачи по AB2
RELEASE CAB2 ; Линия AB2
TRANSFER .10,,AB2Er ; Передача на AB2Er
LEAVE ABUF ; Выход из пункта А
ENTER BBUF ; Вход в пункт B
BC2Er SEIZE CBC2 ; Линия BC2
ADVANCE 3,1 ; Время передачи по BC2
RELEASE CBC2 ; Линия BC2
TRANSFER .05,,BC2Er ; Передача на BC2Er
LEAVE BBUF ; Выход из пункта B
*
* Сегмент счетчика
*
OUT TERMINATE 1 ; Пункт C. Выход пакетов из модели
START 500
2.4.2. Описание программы.
2.4.3. Листинг результатов моделирования
GPSS World Simulation Report - #16_end.26.9
Tuesday, May 04, 2005 01:11:51
START TIME END TIME BLOCKS FACILITIES STORAGES
0.000 3014.613 28 4 2
NAME VALUE
AB1 3.000
AB1ER 4.000
AB2 16.000
AB2ER 17.000
ABUF 1.000
BBUF 2.000
BC1ER 10.000
BC2ER 23.000
CAB1 1.000
CAB2 2.000
CBC1 3.000
CBC2 4.000
OUT 28.000
LABEL LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY
1 GENERATE 500 0 0
2 TRANSFER 500 0 0
AB1 3 ENTER 246 0 0
AB1ER 4 SEIZE 281 0 0
5 ADVANCE 281 0 0
6 RELEASE 281 0 0
7 TRANSFER 281 0 0
8 LEAVE 246 0 0
9 ENTER 246 0 0
BC1ER 10 SEIZE 255 0 0
11 ADVANCE 255 0 0
12 RELEASE 255 0 0
13 TRANSFER 255 0 0
14 LEAVE 246 0 0
15 TRANSFER 246 0 0
AB2 16 ENTER 254 0 0
AB2ER 17 SEIZE 277 0 0
18 ADVANCE 277 0 0
19 RELEASE 277 0 0
20 TRANSFER 277 0 0
21 LEAVE 254 0 0
22 ENTER 254 0 0
BC2ER 23 SEIZE 265 0 0
24 ADVANCE 265 0 0
25 RELEASE 265 0 0
26 TRANSFER 265 0 0
27 LEAVE 254 0 0
OUT 28 TERMINATE 500 0 0
FACILITY ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY
CAB1 281 0.271 2.911 1 0 0 0 0 0
CAB2 277 0.285 3.100 1 0 0 0 0 0
CBC1 255 0.254 3.000 1 0 0 0 0 0
CBC2 265 0.259 2.950 1 0 0 0 0 0
STORAGE CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY
ABUF 2 2 0 2 500 1 0.570 0.285 0 0
BBUF 2 2 0 2 500 1 0.518 0.259 0 0
3. Заключение.
После проведения имитационного эксперимент из листинга результатов видно, что максимальные объемы буферов в пунктах А и В:
• пункта А – 2 единицы
• пункта В – 2 единицы
Загрузка пункта А – 29% , а пункта В – 26%. Временные потери, возникающие из-за сбоев в каналах связи:
• по направлению AB1: 35×2.911=101.885
• по направлению BС1: 9×3.000=27.000
• по направлению AB2: 23×3.100=71.300
• по направлению BС2: 11×2.950=32.45
Итого: 232.635 е.м.в. (232.635мс = 0.232635c), а время моделирования равно 3014.613 е.м.в.
Во время выполнения курсовой работы мы заметили, что язык GPSS сильно отличается от алгоритмически языков программирования. Хотя язык GPSS не требует специальной подготовки в области программирования, а наличие интерактивной среды со стандартным интерфейсом, которую система GPSS World, позволяет до минимума свести взаимодействие пользователя с инструментальной ЭВМ и ее операционной системой. Однако построение моделей и организация вычислительного эксперимента требуют некоторых знаний из области теории массового обслуживания, теории вероятностей и математической статистики. |